含隐变量的图模型的参数学习（EM 算法）

有些时候 $X$ 中的变量有很复杂的依赖关系，直接建模 $p(x)$ 会很困难，这时通常会引入隐变量 $z$ 来简化模型。如果图模型中包含隐变量，即有部分变量是不可观测的，这时就需要用 EM 算法（Expectation Maximum，期望最大化算法）来进行参数估计。

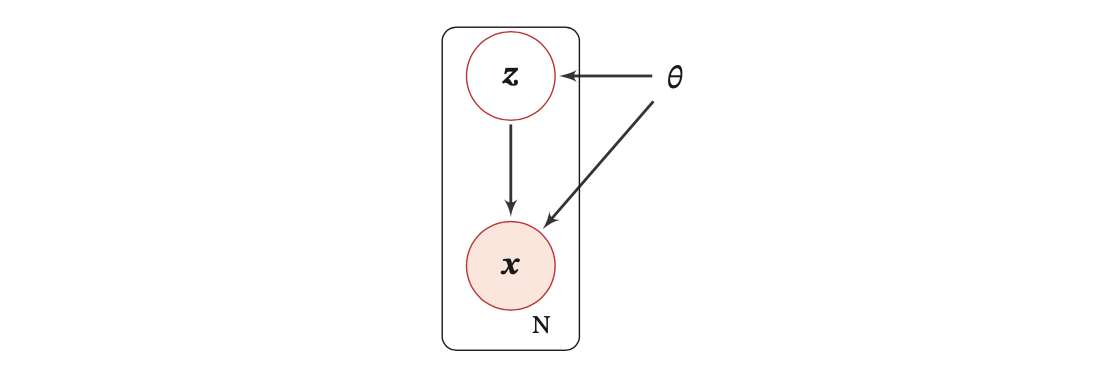
下图为带隐变量的贝叶斯网络的图模型结构，矩形表示其中的变量重复 $N$ 次（因为数据集中有 $N$ 个样本）：

边缘似然

令 $X$ 为可观测变量集合，$Z$ 为隐变量集合。由于隐变量不可观测，因此一般改用边缘分布（也就是显变量的分布）的最大似然为目标函数。

样本 $x$ 的边缘似然函数（Marginal Likelihood）为：

$$p_{\theta }(x)=\sum _z{p}_{\theta }(x,z)=\sum _z{p}_{\theta }(x\mid z)p_{\theta }(z)$$

边缘似然也称为证据（evidence）。

给定 $N$ 个训练样本 $D=\{x^{(n)}{\}}_{n=1}^N$，其对数边缘似然函数为：

$$\begin{array}{rl}L(D;\theta )& =\frac{1}{N}\sum _{n=1}^N\log p_{\theta }(x^{(n)})\\ & =\frac{1}{N}\sum _{n=1}^N\log \sum _z{p}_{\theta }(x^{(n)},z)\\ & =\frac{1}{N}\sum _{n=1}^N\log \sum _z{p}_{\theta }(x^{(n)}\mid z)p_{\theta }(z)\end{array}$$

ELBO

上式第三步意味着我们要对所有可能的 $z$ 求和（或积分），除非 $p_{\theta }(x,z)$ 的形式非常简单，否则这在很多情况下是 intractable 的。因此，为了计算 $\log p_{\theta }(x)$，我们引入一个额外的变分函数（variational function）$q(z)$，$q(z)$ 是一个定义在隐变量 $Z$ 上的分布：

$$\begin{array}{rl}\log p_{\theta }(x)& =\log \sum _{z}q(z)\frac{p_{\theta }(x,z)}{q(z)}\\ & =\log {\mathbb{E}}_{q(z)}[\frac{p_{\theta }(x,z)}{q(z)}]\ge {\mathbb{E}}_{q(z)}[\log \frac{p_{\theta }(x,z)}{q(z)}]\text{（詹森不等式）}\\ & =\sum _{z}q(z)\log \frac{p_{\theta }(x,z)}{q(z)}\\ & \triangleq {\text{ELBO}}_{\theta }(q,x)\end{array}$$

${\text{ELBO}}_{\theta }(q,x)$ 为样本 $x$ 的对数边缘似然函数 $\log p_{\theta }(x)$ 的下界，称为证据下界（Evidence Lower Bound，ELBO）。

其中，詹森不等式（Jensen Inequlity）指，对于下凸函数 $g$，『期望的函数大于等于函数的期望』一定成立，即：

$$g(\mathbb{E}[X])\ge \mathbb{E}[g(X)]$$

当且仅当 $q(z)=p_{\theta }(z\mid x)$ 时，等号成立，即 $\log p_{\theta }(x)={\text{ELBO}}_{\theta }(q,x)$。

---

证明过程如下（《神经网络与深度学习》习题 11-4，不想看证明的话跳过就好）：

显然，当且仅当 $\frac{p_{\theta }(x,z)}{q(z)}$ 的比值为一个常数时，等号成立：

$$\frac{p_{\theta }(x,z)}{q(z)}=c\text{\hspace{1em}(1)}$$

$$\Rightarrow p_{\theta }(x,z)=c\cdot q(z)$$

$$\Rightarrow {\int }_z{p}_{\theta }(x,z)dz={\int }_{z}c\cdot q(z)dz$$

其中 ${\int }_z{p}_{\theta }(x,z)dz$ 可以看作是 $p_{\theta }(x)$ 的边缘概率；${\int }_{z}c\cdot q(z)dz$ 可以看作是 $c$ 的边缘概率，从而：

$$p_{\theta }(x)=c\text{\hspace{1em}(2)}$$

将式 (2) 带入式 (1) 得：

$$q(z)=\frac{p_{\theta }(x,z)}{p_{\theta }(x)}=p_{\theta }(z\mid x)\text{\hspace{1em}(3)}$$

注意，式 (3) 中的 $\theta$ 是一个常数值。比如当 EM 算法的第 $t$ 步 $\arg {\max }_{{\theta }_t}{p}_{{\theta }_{t+1}}(x)$ 时，式 (3) 中的 $\theta$ 就是 $t-1$ 步时的参数 ${\theta }_t$。

---

这样，最大化对数边缘似然函数 $\log p_{\theta }(x)$ 的过程可以分解为两个步骤：

1. 找到近似分布 $q(z)$ 使得 $\log p_{\theta }(x)={\text{ELBO}}_{\theta }(q,x)$

2. 寻找能最大化 ${\text{ELBO}}_{\theta }(q,x)$ 的参数 $\theta$

这就是 EM 算法。

EM 算法

EM 算法具体分为 E 步（expectation step）和 M 步（maximization step），这两步不断重复，通过迭代的方法来最大化边缘似然。在第 $t$ 步更新时，E 步和 M 步分别为：

1. E 步：固定参数 ${\theta }_t$ ，找到一个分布 $q_{t+1}(z)$ 使得证据下界 ${\text{ELBO}}_{{\theta }_t}(q,x)$ 等于 $\log p_{{\theta }_t}(x)$

2. M 步：固定 $q_{t+1}(z)$，找到一组参数使得证据下界 ${\text{ELBO}}_{{\theta }_t}(q_{t+1},x)$ 最大，即：

$$\begin{array}{rl}{\theta }_{t+1}& =\arg \underset{\theta }{\max }{\text{ELBO}}_{\theta }(q_{t+1},x)\\ & =\arg \underset{\theta }{\max }\sum _z{q}_{t+1}(z)\log \frac{p_{\theta }(x,z)}{q_{t+1}(z)}\\ & =\arg \underset{\theta }{\max }\sum _z{p}_{{\theta }_t}(z\mid x)\log \frac{p_{\theta }(x,z)}{p_{{\theta }_t}(z\mid x)}\\ & =\arg \underset{\theta }{\max }\sum _z{p}_{{\theta }_t}(z\mid x)\log p_{\theta }(x,z)\end{array}$$

${\theta }_t$ 为上一时刻的参数，$p_{{\theta }_t}(z\mid x)$ 是 $z$ 的后验分布。

从 KL 散度来理解

对数边缘似然 $\log p_{\theta }(x)$ 可以分解为：

$$p_{\theta }(x,z)=p_{\theta }(z\mid x)p_{\theta }(x)$$

$$\Rightarrow \log p_{\theta }(x,z)=\log p_{\theta }(z\mid x)+\log p_{\theta }(x)$$

$$\Rightarrow \log p_{\theta }(x)=\log p_{\theta }(x,z)-\log p_{\theta }(z\mid x)$$

两边同时对隐变量分布 $q(z)$ 求期望，左边：

$$\sum _{z}q(z)\log p_{\theta }(x)=\log p_{\theta }(x)\sum _{z}q(z)=\log p_{\theta }(x)$$

右边可以先写成：

$$\log p_{\theta }(x,z)-\log p_{\theta }(z\mid x)$$

$$=(\log p_{\theta }(x,z)-\log q(z))-(\log p_{\theta }(z\mid x)-\log q(z))$$

$$=\log \frac{p_{\theta }(x,z)}{q(z)}-\log \frac{p_{\theta }(z\mid x)}{q(z)}$$

则右边对隐变量分布 $q(z)$ 求期望：

$$\sum _{z}q(z)(\log p_{\theta }(x,z)-\log p_{\theta }(z\mid x))$$

$$=\sum _{z}q(z)\log \frac{p_{\theta }(x,z)}{q(z)}-\sum _{z}q(z)\log \frac{p_{\theta }(z\mid x)}{q(z)}$$

$$={\text{ELBO}}_{\theta }(q,x)+\text{KL}(q(z)\Vert p_{\theta }(z\mid x))$$

合起来：

$$\log p_{\theta }(x)={\text{ELBO}}_{\theta }(q,x)+\text{KL}(q(z)\Vert p_{\theta }(z\mid x))$$

其中，$\text{KL}(q(z)\Vert p_{\theta }(z\mid x))$ 为隐变量分布 $q(z)$ 和后验分布 $p_{\theta }(z\mid x)$ 的 KL 散度。

KL 散度一定 $\ge 0$，且当且仅当 $q(z)=p_{\theta }(z\mid x)$ 时，$\text{KL}(q(z)\Vert p_{\theta }(z\mid x))=0$，从而使得 ${\text{ELBO}}_{\theta }(q,x)=\log p_{\theta }(x)$。

所以 ${\text{ELBO}}_{\theta }(q,x)$ 为 $\log p_{\theta }(x)$ 的一个下界。因此当逐步提高这个下界时，相当于增大了 $\log p_{\theta }(x)$，所以要对 ELBO 求期望最大化：

$$\hat{\theta }=\arg \underset{\theta }{\max }{\text{ELBO}}_{\theta }(q,x)$$

收敛性证明

直觉上的证明

假设在第 $t$ 步时的模型参数为 ${\theta }_t$。

• E 步：找到一个分布 $q_{t+1}(z)$ 使得 $\log p_{{\theta }_t}(x)={\text{ELBO}}_{{\theta }_t}(q_{t+1},x)$

• M 步：固定 $q_{t+1}(z)$，找到一组参数 ${\theta }_{t+1}$ 使得 ${\text{ELBO}}_{{\theta }_{t+1}}(q_{t+1},x)$ 最大，则有 ${\text{ELBO}}_{{\theta }_{t+1}}(q_{t+1},x)\ge {\text{ELBO}}_{{\theta }_t}(q_{t+1},x)$

因此有：

$$\log p_{{\theta }_{t+1}}(x)\ge {\text{ELBO}}_{{\theta }_{t+1}}(q_{t+1},x)\ge {\text{ELBO}}_{{\theta }_t}(q_{t+1},x)=\log p_{{\theta }_t}(x)$$

公式上的证明

我觉得直觉上的证明已经很清楚了...所以公式上的证明我就直接放个链接了。

EM 算法在 GMM 中的应用

参考

• 从最大似然到EM算法：一致的理解方式
• 统计学习方法 — EM 算法