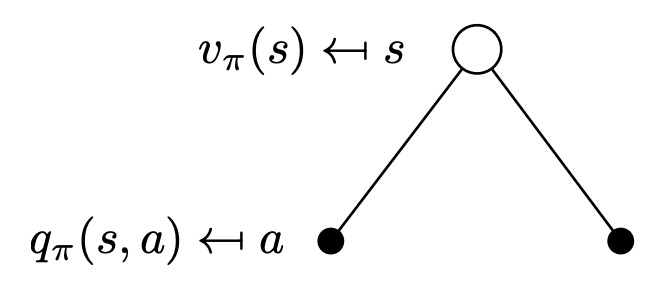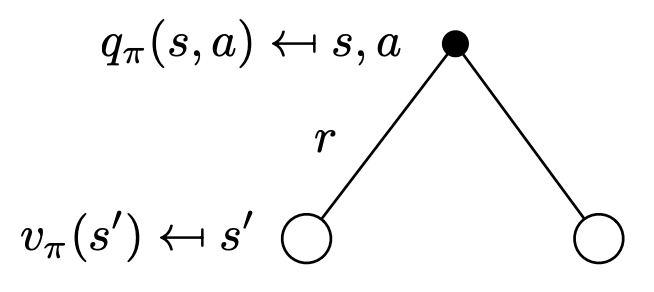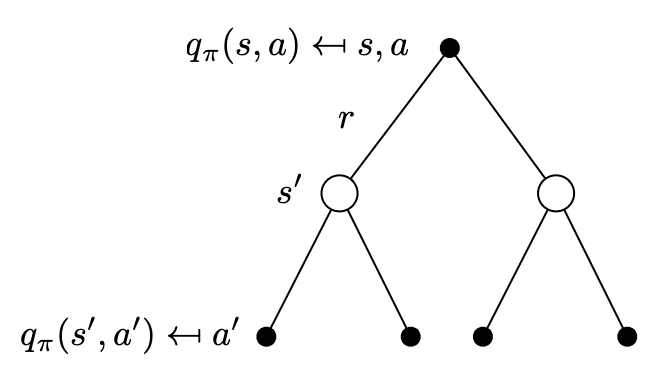贝尔曼方程
贝尔曼方程(Bellman Equation)把值函数分解为了当前奖励(immediate reward)+ 未来奖励的折扣总和(discounted sum of future rewards)。
贝尔曼方程是一个递归的形式。
动作值函数的贝尔曼方程
动作值函数的贝尔曼方程
Qπ(st,at)=ESt+1,At+1[Rt+γ⋅Qπ(St+1,At+1)∣St=st,At=at]
证明过程
易证:
Gt=k=0∑γkRt+k=Rt+γ⋅Gt+1
那么有:
Qπ(st,at)=ESt+1,At+1,⋯[Gt∣St=st,At=at]=ESt+1,At+1,⋯[Rt+γ⋅Gt+1∣St=st,At=at]=ESt+1,At+1,⋯[Rt+γ⋅Qπ(St+1,At+1)∣St=st,At=at]
最后一步是因为动作值函数 Qπ(St+1,At+1) 求的就是 Gt+1 的期望。
状态值函数的贝尔曼方程
状态值函数的贝尔曼方程
Vπ(st)=EAt,St+1[Rt+γ⋅Vπ(St+1)∣St=st]
证明过程
由状态值函数的定义:Vπ(St)=EAt[Qπ(St,At)] 得到:
Qπ(St,At)=ESt+1,At+1[Rt+γ⋅Qπ(St+1,At+1)∣St=st,At=at]=ESt+1[Rt+γ⋅Vπ(St+1)∣St=st,At=at]
Vπ(St)=EAt[Qπ(St,At)]=EAt,St+1[Rt+γ⋅Vπ(St+1)∣St=st]
另一种形式
贝尔曼方程可以表达为另一种形式。
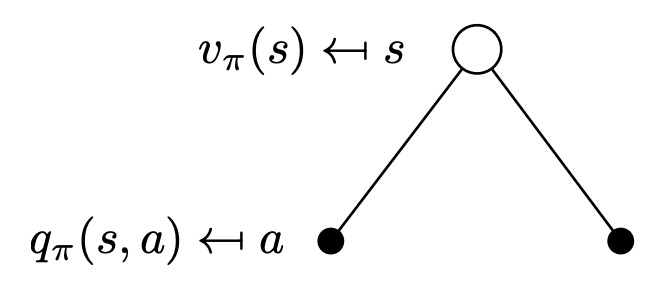
Vπ(s)=a∈A∑π(a∣s)Qπ(s,a)(1)
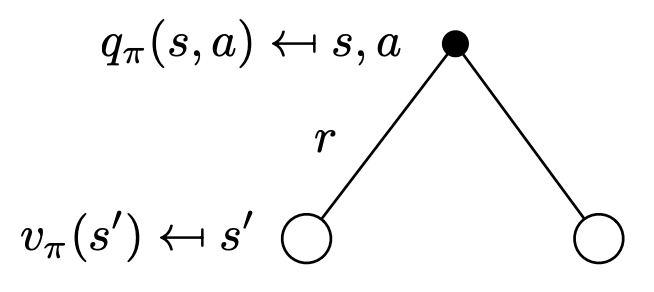
Qπ(s,a)=R(s,a)+γs′∈S∑Pss′aVπ(s′)(2)
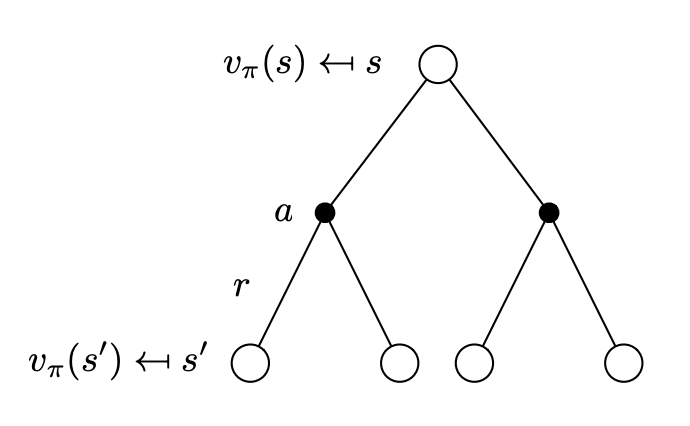
把式 (2) 代入式 (1):
Vπ(s)=a∈A∑π(a∣s)(R(s,a)+γs′∈S∑Pss′aVπ(s′))(3)
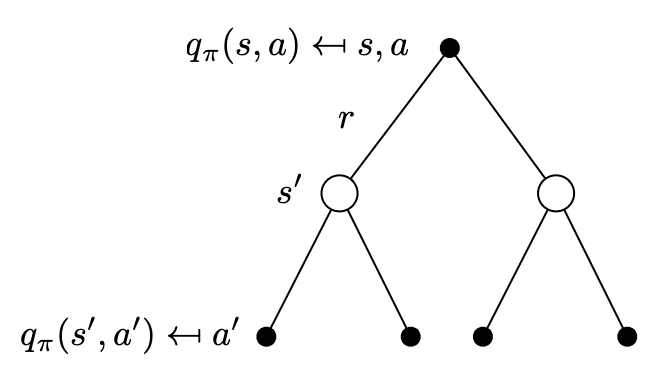
把式 (1) 代入式 (2):
Qπ(s,a)=R(s,a)+γs′∈S∑Pss′aa∈A∑π(a′∣s′)Qπ(s′,a′)(4)
式 (3) 和式 (4) 就是贝尔曼方程的另一种形式。
贝尔曼最优方程
之前定义了最优状态值函数 V∗(s) 和最优动作值函数 Q∗(s,a),如果只关注最优值:
V∗(s)=a∈A∑π(a∣s)Q∗(s,a)
Q∗(s,a)=R(s,a)+γs′∈S∑Pss′aV∗(s′)
V∗(s)=a∈A∑π(a∣s)(R(s,a)+γs′∈S∑Pss′aV∗(s′))(5)
Q∗(s,a)=R(s,a)+γs′∈S∑Pss′aa∈A∑π(a′∣s′)Q∗(s′,a′)(6)
式 (5) 和式 (6) 就是贝尔曼最优方程(Bellman Optimality Equation)。
总结
贝尔曼方程是大多数强化学习算法的理论基础。
可以看到,如果环境是已知的,即 R(s,a) 和 Pss′a 已知,这就变成了一个动态规划问题。但在很多问题中,我们并不知道这两个函数,所以不能直接通过贝尔曼方程来求解。