基本概念

概述

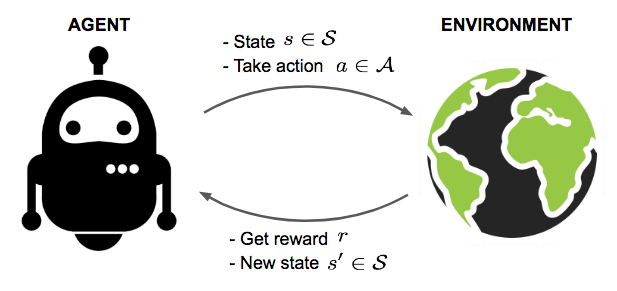
现在有一个智能体（agent）和一个复杂不确定的环境（environment）。智能体会从环境里面获取到当前状态（state）（$s\in \mathcal{S}$），根据这个状态，智能体会根据某种策略 $\pi$（policy）来输出一个动作（action）（$a\in \mathcal{A}$）。然后环境会根据智能体采取的动作和奖励函数 $R$，返回给智能体一个奖励（reward）（$r\in \mathcal{R}$）。环境会怎么对动作进行反馈是由一个模型（model）来定义的，这个模型可能是已知的，也可能是未知的。然后智能体会根据转移概率 $P$（transition function）转移到一个新的状态。

强化学习（Reinforcement Learning）的目标就是，让智能体通过不断的尝试和获得反馈，学习到一个最优策略，从而最大化它能获得的累计奖励 $G$（cumulative future reward），也被叫做回报（return）。

Model-Based / Model-Free

首先是 model-free 和 mode-based 的区别，需要理解的是强化学习中的 model 跟智能体没有关系，model 只跟环境有关，它决定了奖励函数 $R$ 和转移概率 $P$。因此：

• model-based：已知环境，即已知转移概率和奖励函数，那么可以用动态规划（dynamic programming）来解决问题
• model-free：未知环境

回合与轨迹

对于时间步 $t=1,2,\dots ,T$，轨迹（trajectory）是指一个回合（episode）中，智能体观测到的所有的状态、动作、奖励序列：

$$s_1,a_1,r_2,s_2,a_2,\dots ,s_T$$

状态转移概率与奖励函数

model 是对环境的描述，它包含两个部分：转移概率 $P$ 与奖励函数 $R$。

假设智能体目前处于状态 $s$，然后它采取了一个动作，并转移到了状态 $s^{\prime }$，并得到了一个奖励 $r$，我们可以把这一步表示为：$(s,a,s^{\prime },r)$。

转移概率 $P$ 是一个条件概率密度函数，它表示了在状态 $s$ 采取动作 $a$，能转移到状态 $s^{\prime }$ 并得到奖励 $r$ 的概率：

$$P(s^{\prime },r\mid s,a)=\mathbb{P}(S_{t+1}=s^{\prime },R_{t+1}=r\mid S_t=s,A_t=a)$$

而状态转移概率 $P_{s{s}^{\prime }}^a$（state-transition function）消去了奖励这一项，表示在状态 $s$ 采取动作 $a$，能转移到状态 $s^{\prime }$ 的概率：

$$P_{s{s}^{\prime }}^a=P(s^{\prime }\mid s,a)=\mathbb{P}(S_{t+1}=s^{\prime }\mid S_t=s,A_t=a)=\sum _{r\in \mathcal{R}}P(s^{\prime },r\mid s,a)$$

奖励函数 $R$ 估计了在状态 $s$ 采取动作 $a$ 后能得到的奖励的期望：

$$R(s,a)=\mathbb{E}(R_{t+1}\mid S_t=s,A_t=a)=\sum _{r\in \mathcal{R}}r\sum _{s^{\prime }\in \mathcal{S}}P(s^{\prime },r\mid s,a)$$

回报与折扣

强化学习最大化的是回报 $G$，也叫累计奖励。回报是从当前时刻 $t$ 开始到一回合结束的所有折扣奖励的总和：

$$G_t=R_{t+1}+\gamma R_{t+2}+\cdots =\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}$$

$\gamma \in (0,1]$ 是一个超参数折扣因子（discount factor），它会给未来的奖励打折扣，越久远的未来的奖励的折扣越大，因为：

• 越是未来的奖励不确定性越大（比如股市）
• 未来的奖励对当下并没有用，比如你现在给我一万块，或是一年后给我一万块，那我肯定选择现在就把一万块拿了
• 不打折扣的话就需要考虑无限的时间步
• 有些马尔可夫过程是带环的，它并没有终结的时候，我们想避免这个无穷的奖励

策略函数与值函数

策略函数和状态值函数都是在强化学习中需要学习的东西。

策略函数

策略函数 $\pi (s_t)$（一个条件概率密度函数）会控制智能体根据当前状态 $s_t$ 来选择最优动作，从而最大化累计奖励（即回报）。需要注意的是最大化的是累积奖励而不是当前奖励。

策略函数可能是随机策略（stochastic policy function），也可能是确定策略（deterministic policy function）：

• 随机策略：$\pi (a\mid s)=\mathbb{P}[A=a\mid S=s]$
• 确定策略：$\pi (s)=a$

动作值函数

之前已经给出了回报 $G$ 的定义，它是 $t$ 时刻之后所有奖励的加权和。但在 $t$ 时刻我们并不知道 $G_t$ 的值，此时 $G_t$ 仍然是个随机变量，它的随机性来源于 $t$ 时刻之后的状态和动作 $S_{t+1},A_{t+1},\cdots$，而这些状态和动作是有 $\pi$ 决定的。

因此动作值函数（action-value function，“Q-value”）会对 $G_t$ 关于变量 $S_{t+1},A_{t+1},\cdots$ 求条件期望：

$$\begin{array}{rl}{Q}_{\pi }(s_t,a_t)& ={\mathbb{E}}_{S_{t+1},A_{t+1},\cdots }[G_t\mid S_t=s_t,A_t=a_t]\\ & ={\mathbb{E}}_{\pi }[G_t\mid S_t=s_t,A_t=a_t]\end{array}$$

动作值函数依赖于当前状态 $s_t$、当前动作 $a_t$ 和策略 $\pi$。

能让动作值函数最大的策略就是最优策略：

$${\pi }_{\ast }=\arg \underset{\pi }{\max }{Q}_{\pi }(s_t,a_t)$$

还可以定义一个最优动作值函数：

$$Q_{\ast }(s_t,a_t)=\underset{\pi }{\max }{Q}_{\pi }(s_t,a_t)$$

显然有：

$$Q_{{\pi }_{\ast }}(s_t,a_t)=Q_{\ast }(s_t,a_t)$$

状态值函数

每个状态 $s_t$ 还有一个对应的状态值函数 $V_{\pi }(s_t)$（state-value function），它是动作值函数对当前动作 $A_t$ 求期望：

$$\begin{array}{rl}{V}_{\pi }(s_t)& ={\mathbb{E}}_{A_t\sim \pi (s_t)}[Q_{\pi }(s_t,A_t)]\\ & =\sum _{a\in \mathcal{A}}{Q}_{\pi }(s_t,a)\pi (a\mid s_t)\end{array}$$

状态值函数 $V_{\pi }(s_t)$ 只依赖于策略 $\pi$ 和当前状态 $s_t$，不依赖于动作，因此它评估了策略 $\pi$ 和当前状态 $s_t$ 的好坏。

能让状态值函数最大的策略就是最优策略：

$${\pi }_{\ast }=\arg \underset{\pi }{\max }{V}_{\pi }(s_t)$$

最优状态值函数：

$$V_{\ast }(s_t)=\underset{\pi }{\max }{V}_{\pi }(s_t)$$

显然有：

$$V_{{\pi }_{\ast }}(s_t)=V_{\ast }(s_t)$$

优势函数

动作值函数减状态值函数就是优势函数（advantage function）：

$$A_{\pi }(s_t,a_t)=Q_{\pi }(s_t,a_t)-V_{\pi }(s_t)$$