三元模型的平滑估计

极大似然估计会导致稀疏数据的问题，即使训练集非常大，很多 $c(u,v,w)$ 和 $c(u,v)$ 也会很小，甚至为 0。因此本节将讨论用于缓和数据稀疏问题的平滑估计（Smoothed Estimation），它的核心思想依赖于 lower-order statistical estimates，即用一元和二元模型的估计去平滑三元模型的估计。本节将讨论两种常用方法：线性插值（Linear Interpolation）和 Discounting Methods，以及与装桶（Bucketing）结合的线性插值。

线性插值

定义三元、二元和一元模型的极大似然估计为：

$$q_{ML}(w\mid u,v)=\frac{c(u,v,w)}{c(u,v)}$$

$$q_{ML}(w\mid v)=\frac{c(u,v,w)}{c(v)}$$

$$q_{ML}(w)=\frac{c(u,v,w)}{c()}$$

$c(w)$ 表示单词 $w$ 在训练集中出现的次数，$c(\cdot )$ 表示训练集中所有单词的数量。

它们有各自的优缺点：一元模型估计出的参数的分子和分母一定会大于 0（因为每个词在训练集中都至少出现了一次），但它完全忽视了上下文信息。而三元模型考虑了上下文信息，但很多参数会被估计为 0，数据更稀疏。二元模型则介于两者之间。

因此线性插值（Linear Interpolation）的思想是把三种估计加权平均，定义三元估计为：

$$q(w\mid u,v)={\lambda }_1\times q_{ML}(w\mid u,v)+{\lambda }_2\times q_{ML}(w\mid v)+{\lambda }_3\times q_{ML}(w)$$

其中 ${\lambda }_1\ge 0,{\lambda }_2\ge 0,{\lambda }_3\ge 0$，且 ${\lambda }_1+{\lambda }_2+{\lambda }_3=1$。

 

估计 $\lambda$ 的值有多种方式，一种常见的方法是：假设我们有一些不同于训练集和测试集的额外的数据，称之为验证集（development set/validation set）。$c^{\prime }(u,v,w)$ 为三元组 $(u,v,w)$ 在验证集中出现的次数。则验证集上的 log-likelihood（对数似然函数值）为：

$$L({\lambda }_1,{\lambda }_2,{\lambda }_3)=\sum _{u,v,w}{c}^{\prime }(u,v,w)\log q(w\mid u,v)$$

$$=\sum _{u,v,w}{c}^{\prime }(u,v,w)\log ({\lambda }_1\times q_{ML}(w\mid u,v)+{\lambda }_2\times q_{ML}(w\mid v)+{\lambda }_3\times q_{ML}(w))$$

我们要选择使 $L({\lambda }_1,{\lambda }_2,{\lambda }_3)$ 尽可能大，且满足 ${\lambda }_1\ge 0,{\lambda }_2\ge 0,{\lambda }_3\ge 0$，${\lambda }_1+{\lambda }_2+{\lambda }_3=1$ 的 $\lambda$ 值：

$$\arg \underset{{\lambda }_1,{\lambda }_3,{\lambda }_3}{\max }L({\lambda }_1,{\lambda }_2,{\lambda }_3)$$

 

综上，我们引入了三个平滑参数 ${\lambda }_1,{\lambda }_2,{\lambda }_3$，这三个参数可以被理解为是三元、二元、一元极大似然估计的置信度或权重。比如，如果 ${\lambda }_1$ 的值非常接近于 1 ，则意味着我们认为 $q_{ML}(w\mid u,v)$ 的意义很大；相反，如果 ${\lambda }_1$ 接近于 0，则意味我们认为 $q_{ML}(w\mid u,v)$ 的意义不大。

在实际操作中，我们应该让 ${\lambda }_1,{\lambda }_2,{\lambda }_3$ 根据不同的二元组 $(u,v)$ 进行改变。具体来说，当 $c(u,v)$ 更大时，我们应该将 ${\lambda }_1$ 变得更大。因为我们认为当 $c(u,v)$ 较大时，应该给三元估计更高的置信度。

需要保证当 $c(u,v)=0$ 时，${\lambda }_1=0$。因为此时 $q_{ML}(w\mid u,v)=\frac{c(u,v,w)}{c(u,v)}$ 的分母为 0，三元极大似然估计的无法定义。同样，如果 $c(u,v)$ 和 $c(v)$ 都为 0，那么需要保证 $ \lambda_1 = \lambda_2 = 0$，因为此时三元和二元极大似然估计都无法定义。

 

另一种更简单的定义 $\lambda$ 的方法是：

$${\lambda }_1=\frac{c(u,v)}{c(u,v)+\gamma }$$

$${\lambda }_2=(1-{\lambda }_1)\times \frac{c(v)}{c(v)+\gamma }$$

$${\lambda }_3=1-{\lambda }_1-{\lambda }_2$$

$\gamma >0$ 是该方法中唯一的参数。这种方法可以保证 ${\lambda }_1\ge 0,{\lambda }_2\ge 0,{\lambda }_3\ge 0$ 和 ${\lambda }_1+{\lambda }_2+{\lambda }_3=1$。

${\lambda }_1$ 会随着 $c(u,v)$ 的增大而增大，${\lambda }_2$ 会随着 $c(v)$ 的增大而增大。如果 $c(u,v)=0$，则有 ${\lambda }_1=0$；如果 $c(v)=0$，则有 ${\lambda }_2=0$。$\gamma$ 依然取能最大化验证集上的 log-likelihood 的值。

这种决定参数的方式非常粗糙，而且一般情况下并不是最优的。但它足够简单，且有较好的实际应用效果。

Discounting Methods

先考虑一下二元模型的估计，目标是对任意 $w\in \mathcal{V}\cup \{\text{STOP}\}$，$v\in \mathcal{V}\cup \{\ast \}$，估计出 $q(w\mid v)$。

对任意 $c(v,w)>0$，定义 discounted counts 为：

$$c^{\ast }(v,w)=c(v,w)-\beta$$

$\beta$ 的值在 0 到 1 之间（一般取 $\beta =0.5$）。减去 $\beta$ 是因为如果完全使用训练集中的统计数据，会导致高估训练集中出现过的二元组的概率，低估训练集中未出现过的二元组的概率。

对任意满足 $c(u,v)>0$ 的二元组 $(u,v)$，定义：

$$q(w\mid v)=\frac{c^{\ast }(v,w)}{c(v)}$$

相当于在分子上减去了 discounted counts。

如：对以下数据，单词 $the$ 在训练集中出现了 48 次。下表列出了所有满足 $u=the,c(u,v)>0$ 的二元组 $(u,v)$（这些二元组的总数为 48）、所有 discounted counts：$c^{\ast }(x)=c(x)-\beta$（$\beta =0.5$）和所有 $\frac{c^{\ast }(x)}{c(the)}$。

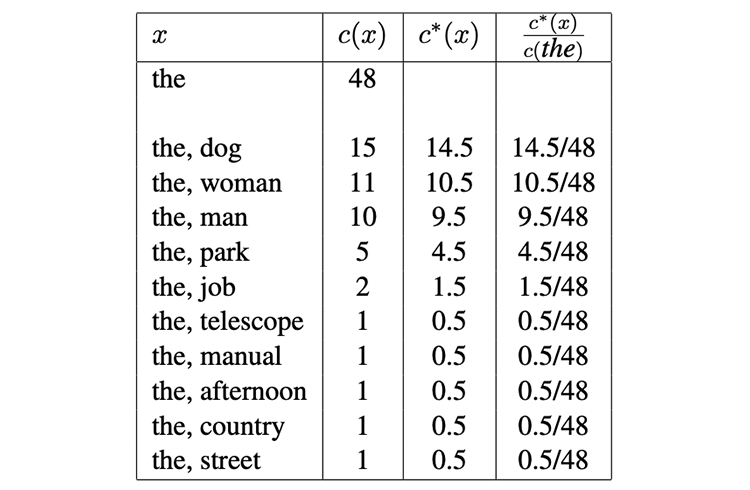
对于所有 $v$，Discounting Methods 都造成了一些概率质量丢失（missing probability mass）：

$$\alpha (v)=1-\sum _{w:c(v,w)>0}\frac{c^{\ast }(v,w)}{c(v)}$$

如上例中：

$$\alpha (the)=1-\sum _{w:c(the,w)>0}\frac{c^{\ast }(the,w)}{c(the)}$$

$$=1-(\frac{14.5}{48}+\frac{10.5}{48}+\frac{9.5}{48}+\frac{4.5}{48}+\frac{1.5}{48}+5\times +\frac{0.5}{48})=1-\frac{43}{48}=\frac{5}{48}$$

这些丢失的质量应该是属于 $c(u,w)=0$ 的。

 

因此，这种估计方法的完整定义如下，令：

$$\mathcal{A}(v)=\{w:c(v,w)>0\}$$

$$\mathcal{B}(v)=\{w:c(v,w)=0\}$$

如上例中，有：

$$\mathcal{A}(v)=\{\text{dog, woman, man, park, job, telescope, manual, afternoon, country, street}\}$$

而 $\mathcal{B}(v)$ 包括词典中剩下额单词。

则该估计的定义为：

$$q_D(w\mid v)=\{\begin{array}{ll}\frac{c^{\ast }(v,w)}{c(v)}& \text{if }w\in \mathcal{A}(v)\\ \alpha (v)\times \frac{q_{ML}(w)}{{\sum }_{w\in \mathcal{B}(v)}{q}_{ML}(w)}& \text{if }w\in \mathcal{B}(v)\end{array}$$

 

这种方法可以推广到三元模型，对任意二元组 $(u,v)$，定义：

$$\mathcal{A}(u,v)=\{w:c(u,v,w)>0\}$$

$$\mathcal{B}(u,v)=\{w:c(u,v,w)=0\}$$

定义三元组 $(u,v,w)$ 的 discounted counts 为：

$$c^{\ast }(u,v,w)=c(u,v,w)-\beta$$

则三元估计为：

$$q_D(w\mid u,v)=\{\begin{array}{ll}\frac{c^{\ast }(u,v,w)}{c(u,v)}& \text{if }w\in \mathcal{A}(u,v)\\ \alpha (u,v)\times \frac{q_{ML}(w\mid v)}{{\sum }_{w\in \mathcal{B}(u,v)}{q}_{ML}(w\mid v)}& \text{if }w\in \mathcal{B}(u,v)\end{array}$$

其中：

$$\alpha (u,v)=1-\sum _{w\in \mathcal{A}(u,v)}\frac{c^{\ast }(u,v,w)}{c(u,v)}$$

 

$\beta$ 是该方法中唯一的参数，跟线性插值模型一样，一般也是用能最大化 development data 上的 log-likelihood $\beta$。定义 $c^{\prime }(u,v,w)$ 为三元组 $u,v,w$ 在 development data 中出现的次数，development data 上的 log-likelihood 为： ${\sum }_{u,v,w}{c}^{\prime }(u,v,w)\log q_D(w\mid u,v)$$q_D(w\mid u,v)$ 会随着 $\beta$ 的变化而变化，一般我们会尝试一系列可能的 $\beta$ 值，如 $\{0.1,0.2,...,0.9\}$，对每个 $\beta$ 值都计算一遍 development data 上的 log-likelihood，最后选择能最大化 development data 上的 log-likelihood 的 $\beta$。

线性插值 + bucketing

线性插值模型中参数估计的定义为：

$$q(w\mid u,v)={\lambda }_1\times q_{ML}(w\mid u,v)+{\lambda }_2\times q_{ML}(w\mid v)+{\lambda }_3\times q_{ML}(w)$$

当 $c(u,v)$ 更大时，我们应该将 ${\lambda }_1$ 变得更大；同样，当 $c(v)$ 更大时，也应该将 ${\lambda }_2$ 变得更大。一个实现这个目标的典型方法是 bucketing。

第一步是定义一个函数 $\Pi$，它将二元组 $(u,v)$ 映射到值 $\Pi (u,v)\in \{1,2,...,K\}$，$K$ 是指定的 bucket 的数量。也就是说函数 $\Pi$ 将二元组 $(u,v)$ 划分为了 $K$ 个不同的子集。这个函数是手动定义的，它通常取决于不同二元组在训练集中的出现频率。

如：

$$\begin{array}{rl}\Pi (u,v)=1& \text{if }100\le c(u,v)\\ \Pi (u,v)=2& \text{if }50\le c(u,v)<100\\ \Pi (u,v)=3& \text{if }20\le c(u,v)<50\\ \Pi (u,v)=4& \text{if }10\le c(u,v)<20\\ \Pi (u,v)=5& \text{if }5\le c(u,v)<10\\ \Pi (u,v)=6& \text{if }2\le c(u,v)<5\\ \Pi (u,v)=7& \text{if }c(u,v)=1\\ \Pi (u,v)=8& \text{if }c(u,v)=0\text{ and }c(v)>0\\ \Pi (u,v)=9& \text{otherwise}\end{array}$$

然后我们对所有 $k\in \{1,2,...,K\}$ 引入平滑参数 ${\lambda }_1^{(k)},{\lambda }_2^{(k)},{\lambda }_3^{(k)}$，因此每个 bucket 都会有一组自己的平滑参数。这些平滑参数同样需要满足 ${\lambda }_1^{(k)}\ge 0,{\lambda }_2^{(k)}\ge 0,{\lambda }_3^{(k)}\ge 0,{\lambda }_1^{(k)}+{\lambda }_2^{(k)}+{\lambda }_3^{(k)}=1$。

则线性插值估计的定义为：

$$q(w\mid u,v)={\lambda }_1^{(k)}\times q_{ML}(w\mid u,v)+{\lambda }_2^{(k)}\times q_{ML}(w\mid v)+{\lambda }_3^{(k)}\times q_{ML}(w)$$

其中 $k\in \Pi (u,v)$。

因此，平滑参数依赖于 $\Pi (u,v)$ 的值，而 $\Pi (u,v)$ 依赖于 $c(u,v)$ 和 $c(v)$。

 

平滑参数还是取能最大化验证集上的 log-likelihood 的值。定义 $c^{\prime }(u,v,w)$ 为三元组 $u,v,w$ 在验证集中出现的次数，则验证集上的的 log-likelihood 为：

$$\sum _{u,v,w}{c}^{\prime }(u,v,w)\log q(w\mid u,v)$$

$$=\sum _{u,v,w}{c}^{\prime }(u,v,w)\log ({\lambda }_1^{(\Pi (u,v))}\times q_{ML}(w\mid u,v)+{\lambda }_2^{(\Pi (u,v))}\times q_{ML}(w\mid v)+{\lambda }_3^{(\Pi (u,v))}\times q_{ML}(w))$$

$$=\sum _{k=1}^K\sum _{u,v,w:\Pi (u,v)=k}{c}^{\prime }(u,v,w)\log ({\lambda }_1^{(k)}\times q_{ML}(w\mid u,v)+{\lambda }_2^{(k)}\times q_{ML}(w\mid v)+{\lambda }_3^{(k)}\times q_{ML}(w))$$

然后取能最大化这个值的 ${\lambda }_1^{(k)},{\lambda }_2^{(k)},{\lambda }_3^{(k)}$。